R3 publishes a new post-quantum signature algorithm tailored to blockchains

Quantum Computers

Before we explain the superiority of BPQS and why it was likely to be invented by a blockchain company, like R3, let’s first take a quick look at current state of the art. I am also highlighting that when we hear the word “post-quantum” it usually implies an algorithm that still runs on conventional CPUs, however it is carefully designed in a way that we don’t know of any quantum algorithm that can break it (yet). Well, we should better say “quantum-resistant”, but literature usually refers to it as “post-quantum”, so we stick to it.

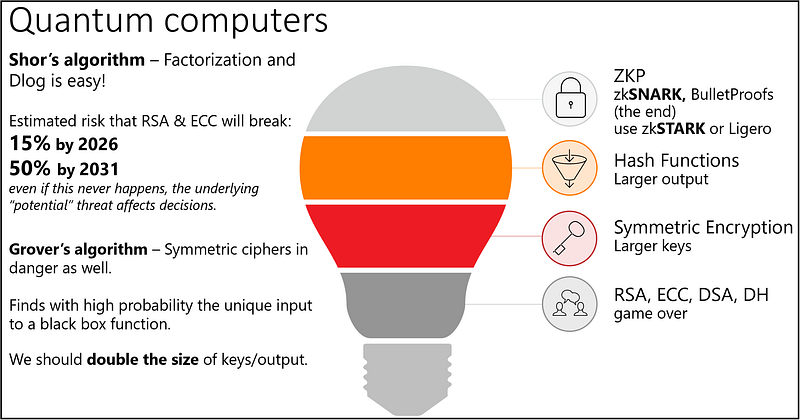
The threat quantum computers pose to classical cryptography has increased the interest in post-quantum research; this is obvious from the increased number of articles dealing with either quantum-based or quantum-resistant solutions. More specifically, due to Shor’s algorithm, a quantum computer could easily factor a big integer in polynomial time, thus effectively break RSA in seconds. Implementations of Shor’s algorithm can also solve discrete logarithms and render today’s digital signatures, such as DSA, ECDSA and EdDSA, useless.

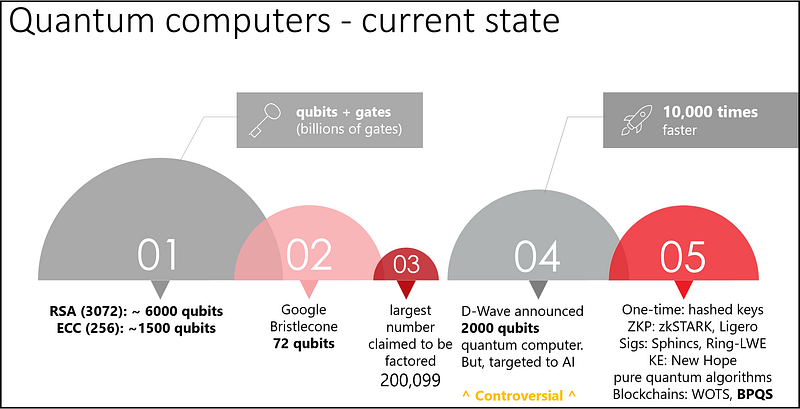
10 years ago there was little evidence of practical quantum computers. But the race has already begun. In 2018, Google unveiled Bristlecone, a new quantum computing chip with 72 qubits, 22 more than the 50-qubit processor announced by IBM in 2017. We should also mention D-Wave, a company that recently announced a 2000-qubit processor optimised for quantum annealing metaheuristics; however, there are reports that D-Wave’s quantum speedup analysis is debatable. To summarise, even though more research and experiments are required to allow for stable quantum chips with low error and noise rates, it is a fact that quantum technology is progressing.

The reality is we have yet to build a computer with the thousands of stable logical qubits required to make classical public key cryptography obsolete. However, some optimistic predictions estimate that a large quantum computer capable of breaking asymmetric cryptography might be available in the next 10 to 20 years. I’m personally more conservative and it might take a bit more than that, but I would highlight that research is driven by market requirements for more time-efficient computing and the ability to solve problems that were previously considered impracticable… and human intelligence usually surprises us.

If the quantum-apocalypse ever happens, the security impact of breaking public key cryptography would be tremendous, as almost everything from HTTPS, VPN
and PKI in general, is basing their authentication, key exchange and digital signatures on classical cryptography. Blockchains would be hit equally hard, and would perhaps be one of the most affected sectors due to direct and untraceable economic incentives.

So, why R3 is exploring post-quantum?

Corda is probably the most “cryptographically” agile blockchain/DLT and since early 2017, users have the option to choose between multiple signing key-types including RSA, ECDSA, EdDSA and SPHINCS. Note that EdDSA is currently the default scheme in Corda, mainly due to its efficiency and security against side-channel attacks. You might not be familiar with the last scheme though, SPHINCS, which is a quantum resistant algorithm, whose construction and security are completely based on hash functions and nothing else; no elliptic curves, no prime numbers, no special maths.

Many of you might not know, but Corda is one of the first blockchains where “obsessed with security” users can sign transactions with post-quantum secure keys. Well, this would make sense especially for long-term contracts, like mortgages and pension schemes. In short, post-quantum algorithms are usually a candidate option in cases where assets should remain locked or inactive for dozens of years.

But, why not use SPHINCS for every transaction? Because there are two major caveats that make it impractical for many blockchain applications: a) its relatively slow signing speed and b) its 41KB signature output.

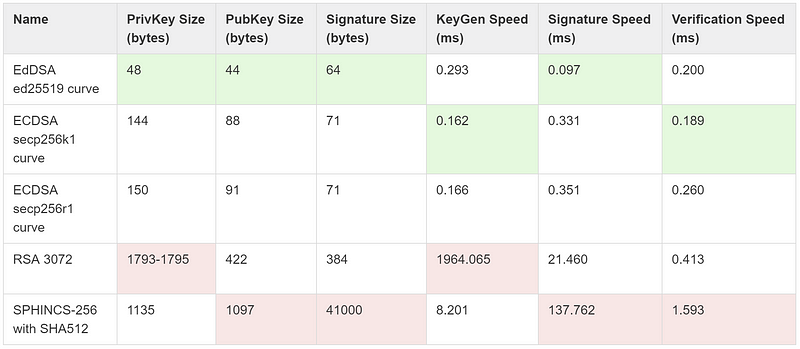
It’s true there have been various attempts in the literature to optimise SPHINCS and we know how to produce shorter signatures by using stateful hash-based solutions, such as XMSS and its variants. We went a step further so as to build an efficient post-quantum scheme tailored to blockchains that we could use in Corda and also influence HSM vendors to eventually support post-quantum solutions for demanding customers and applications.

BPQS is actually a modified XMSS protocol, best suited to two types of application requirements:
a) when signing keys are used once or just a few times (i.e., 3 times). The most common example is one-time addresses, which is the recommended approach in public blockchains
and
b) when there is an underlying immutable graph structure which can serve the role of a global cache, independently on how many times a key is reused. For instance, in permissioned blockchains some entities are known to sign with the same legal-identity key again and again, i.e., notaries or oracles.

Ah, forgot to mention that the crypto agility feature is one of the differentiation factors between Corda and other distributed ledgers. For some reason we don’t advertise it a lot, but one can practically build a new post-quantum token or secure critical contracts requiring multiple signature key-types. The latter is possible via the CompositeKey feature in Corda, where you can apply a “belts and braces” approach and simultaneously sign a transaction with multiple keys, such as ECDSA, RSA and BPQS, so that all of these algorithms should break for your assets to be stolen. A similar combined method was recently explored by Google in their CECPQ1 post-quantum cipher suite TLS experiments.

The misconception: hashed keys to the rescue for existing blockchains, such as Bitcoin and Ethereum.

Most blockchains mitigate the quantum threat by using addresses that are generated from cryptographic hashes of the public keys. This additional layer
of security means that a public key only gets exposed to the ledger after the first transaction that it participates in occurs (i.e., when a Bitcoin is spent). Until this point, only the hashed recipient key (the address) is exposed and consequently attacks such as Shor’s algorithm are not applicable at this stage.

However, the following attack vectors are still applicable, even when hashed keys are utilised:

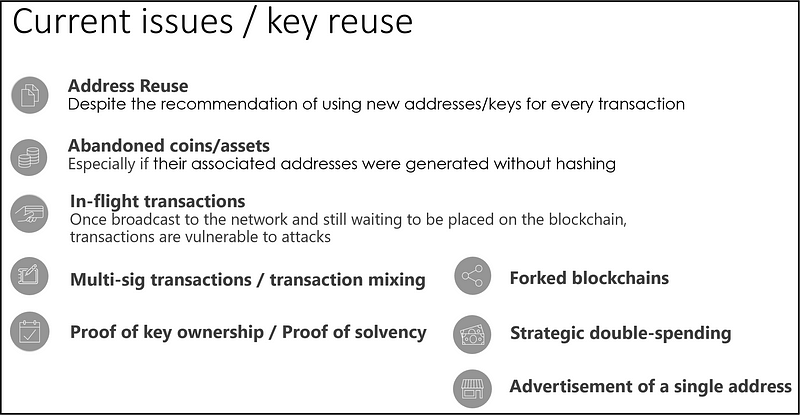
In short, users tend to reuse their keys on purpose, by mistake or some times because they don’t have other options. The most interesting example is forked blockchains, where the same key holds assets in two or more chains and at the time you spend on one of them, the public key gets exposed. In-flight transactions and transaction mixing also reveal the public keys for a few moments, and this time-window will be more than enough to derive the private key when a proper quantum computer gets available.

Hash-Based Signature schemes

BPQS is a hash-based signature and as such, it uses one-time signature (OTS) schemes as a fundamental building block. Unlike most other signature schemes, OTS requires only a secure cryptographic hash function and no other hardness assumption (about a number-theoretic problem) and is not known to be vulnerable to Shor’s algorithm. Secure here refers to either hash collision resistance or mere second pre-image resistance, depending on the specific one-time signature used.

Common examples of one-time signature schemes are the seminal one by Lamport, the Winternitz scheme and its recent variant W-OTS+. In one-time signatures, the private key consists of randomly generated values and the public key is a function of the private key, involving the underlying hash function.

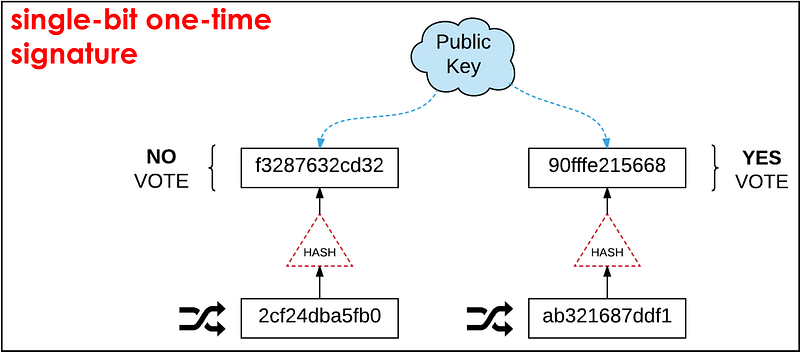
The picture below depicts a very basic voting example where I want to sign one bit of information using Lamport’s algorithm. Briefly,
a) I initially generate two random values and I use them as my private key (in this picture 2cf24dba5fb0 and ab321687ddf1, respectively).
b) Then, I hash both values independently and the resulted outputs form my public key (f3287632cd32 and 90fffe215668).
c) I then publish my two public key parts and we all agree that the left part will correspond to bitValue=0 (i.e., if my vote is NO), while the one on the right corresponds to bitValue=1 (i.e., if my vote is YES).
d) Now, when I actually submit my vote, I will reveal one of the two private keys depending on my choice. As I am the only person who knows these two values, if I publish ab321687ddf1, then every verifier can check that it corresponds to my right public key part, so they can be convinced I voted YES.

If we use the same logic for extra bits of information, we will eventually be able to sign any message. There is an excellent post that explains with easy to follow diagrams how the major hash-based signature schemes work, thus, if you want to learn more, visit this link.

For the time being, I’m not getting into the low-level cryptographic details. But, I need to mention that OTS, as its name states, are inadequate on their own in practice, since each one-time private key can only be used to securely sign a single message. Hm… we’ve already mentioned we might need to reuse a key and sign a second message. Now what?

Blockchained Post-Quantum Signatures

Unfortunately, each time we reuse an OTS key, the advertised bits of security are reduced to half (on average). Surprisingly, there are existing blockchains that assume one-time is enough, which is obviously wrong. IOTA is such an example, and it has been reported that some wallets do not allow you to sign for a second time with the same key. The latter results to asset freezing if for instance the first transaction never goes through. I’m wondering what is the plan in case of a fork, in which case it will be inevitable that one needs to sign at least two times.

Although there are extensions of the simple OTS schemes to allow for multiple times signing, such as SPHINCS, they are not that fast and succinct, while in some cases key generation is very expensive. However, in blockchains, most of the times we need to sign once and in rare cases we need to reuse a key. But because these are exceptional cases, we realised we don’t really need the complexity of schemes like SPHINCS and XMSS, but a fallback key, which will be activated only when we need to sign again.

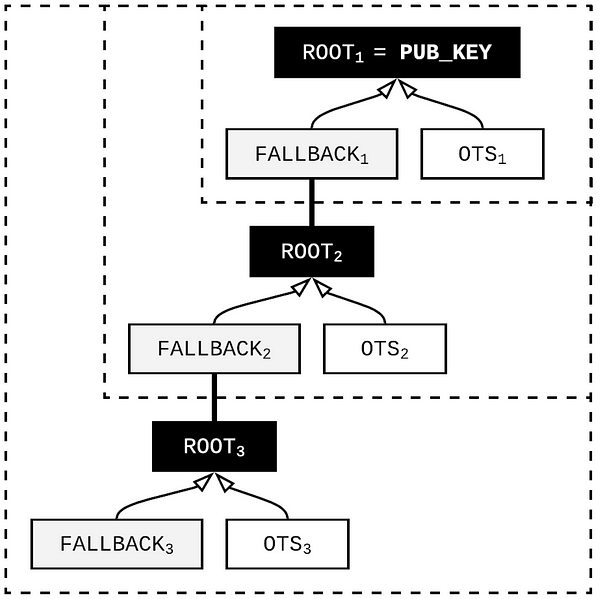
BPQS is actually a chain/path of fallback keys. This way, we always need 2 OTS keys and nothing more. One of them is used to sign the actual message (transaction). The other is the fallback key that will sign a new set of 2 OTS keys and so on…

And what if for any reason I need to sign thousands of times?
Here is the magic behind BPQS, “if you signed in the past and it has been recorded in the blockchain, just provide a link to the block that contains your authentication path”.

Due to above trick, each signature remains very short as previous paths are delegated to existing blocks (which are already verified — so no extra computations). Permissioned blockchains, like Corda, can benefit a lot from the BPQS approach, because notaries and oracles need to sign multiple times with their legal identity keys. If post-quantum security is a requirement, BPQS should definitely be considered.